Vanilla Open-Loop
Consistent but unreactive to cup's motion.
Predicting and executing a sequence of actions without intermediate replanning, known as action chunking, is increasingly used in robot learning from human demonstrations. Yet, its reported effects on the learned policy are inconsistent: some studies find it crucial for achieving strong results, while others observe decreased performance. In this paper, we first dissect how action chunking impacts the divergence between a learner and a demonstrator. We find that action chunking allows the learner to better capture the temporal dependencies in demonstrations but at the cost of reduced reactivity in stochastic environments. To address this tradeoff, we propose Bidirectional Decoding (BID), a test-time inference algorithm that bridges action chunking with closed-loop operations. BID samples multiple predictions at each time step and searches for the optimal one based on two criteria: (i) backward coherence, which favors samples that align with previous decisions; (ii) forward contrast, which seeks samples of high likelihood for future plans. By coupling decisions within and across action chunks, BID promotes consistency over time while maintaining reactivity to unexpected changes. Experimental results show that BID boosts the performance of two state-of-the-art generative policies across seven simulation benchmarks and two real-world tasks.
In action chunking, the agent predicts the joint distribution of a sequence of actions conditioned on the context and then executes all or part of the sequence without replanning. In our analysis, we consider two models with equal context length \( c \) and investigate the effect of using a longer action horizon. Consider a shorter action chunk of length \( h \) and a longer one of length \( h + d \). The longer action chunk benefits from remembering more past states and suffers from having not observed the more recent states, as is illustrated below:
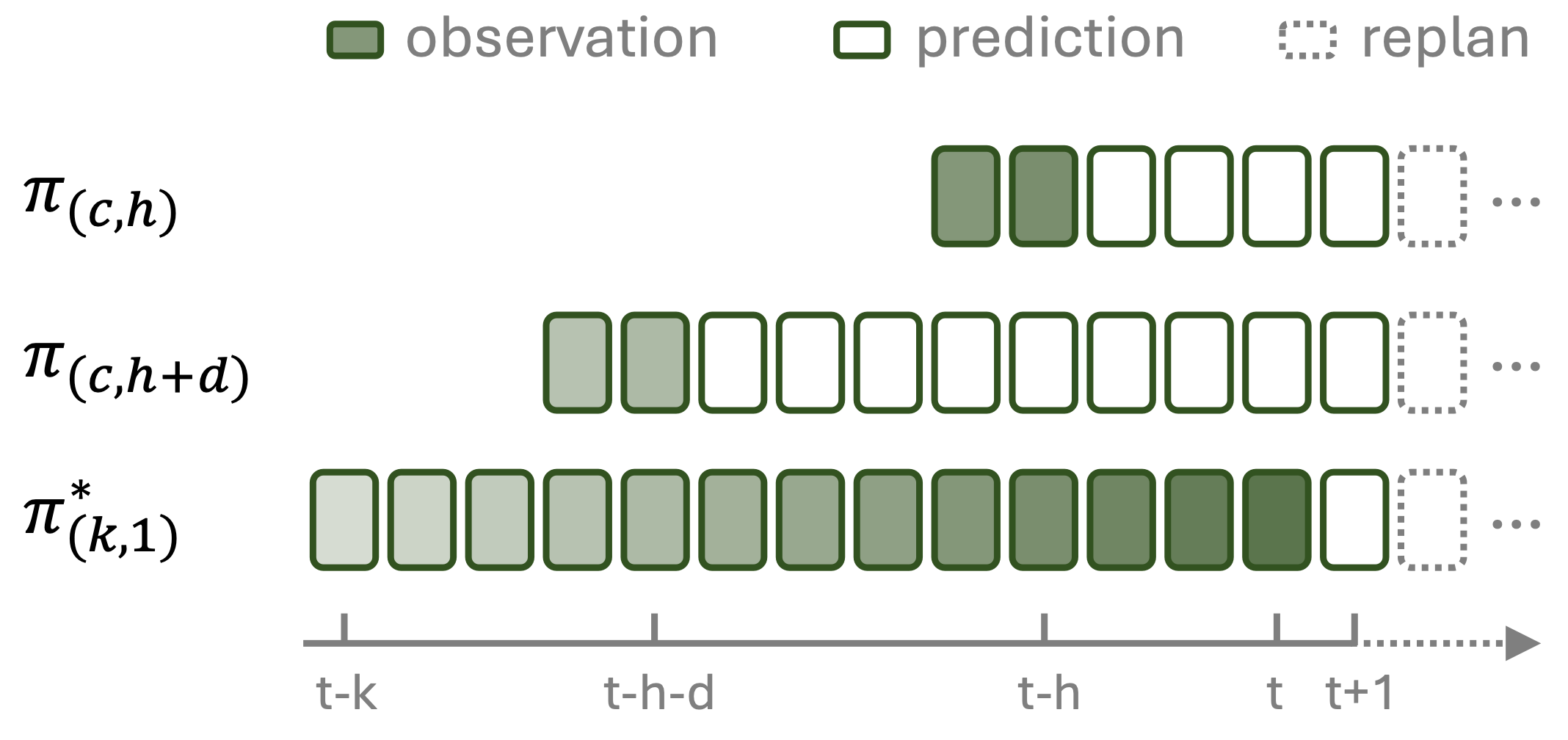
Fig 1: Shaded regions indicate observed history; darker indicate greater influence on current decision.
The expected loss of the two agents with respect to the expert, \( \Delta_d := \min_{\pi_{h+d}} \mathbb{E} \left[\mathcal{L}(\pi_{h+d}, \pi^*) | C \right] - \min_{\pi_{h}} \mathbb{E} \left[\mathcal{L}(\pi_{h}, \pi^*) | C \right] \), are related by the following inequality. $$ \alpha_{f} - \epsilon_{b}\left(1 - \prod_{\tau \in \tau_b}P_b(\tau)(P_b(\tau) + \delta_b(\tau))\right) \leq \Delta_d \leq \epsilon_{f}\left(1 - \prod_{\tau \in \tau_f}P_f(\tau)(P_f(\tau) + \delta_f(\tau))\right) - \alpha_{b}. $$ Intuitively, the advantage of each policy stems from the additional information it has access to (i.e., \( \alpha_f \) for \( \pi_h \) and \( \alpha_b \) for \( \pi_{h+d} \)) while the disadvantage is bounded by the maximum divergence arising from inferring missing information incorrectly. Our theoretical analysis provides us two important takeaways :
Takeaway 1: In deterministic environments, while both policies need to infer the same number of unobserved states, longer action horizon benefits from conditioning on additional actions, which may significantly aid in inferring the corresponding states through its action chunk. However, this is only true if the implicit dynamics model learned by the policy is approximately accurate. Note that \(\pi_{h+d}\) performs better as we increase the diversity of strategies present in the dataset i.e., as the distribution of actions taken by the expert prior to the context of the short horizon policy becomes higher variance.
Takeaway 2: Recent states are often more important to decision making and, therefore, the disadvantages of action chunking become pronounced when inferring these recent states becomes difficult. This can happen if the test environment is stochastic. This can also happen if the test environment is deterministic as long as the implicit dynamics model is inaccurate - either due to a distribution shift or because of learning difficulty.
Takeaway 3: This analysis motivates us to use closed-loop operations, to maximize reactivity to environment stochasticity, while increasing temporal consistency through guided resampling.
We frame the problem of closed-loop action chunking as searching for the optimal action among a batch of samples drawn at each time step, $$ a^* = \arg \min_{a \in \mathcal{A}} \mathcal{L}_B(a) + \mathcal{L}_F(a) $$ where \(\mathcal{A}\) is the set of sampled action chunks, \( \mathcal{L}_B \) and \( \mathcal{L}_F \) are two criteria measuring the temporal dependency with respect to the backward decision and forward plan.
To ensure temporal coherence, we reference the action chunk from the previous time step, \( \hat a := \{ {a}^{(t-1)}_{t-1}, \cdots, {a}^{(t-1)}_{t+l-1} \} \) and minimize the weighted sum of Euclidean distance across \( l - 1 \) overlapping steps:
$$ \mathcal{L}_B = \sum_{\tau=0}^{l-1} \rho^\tau \left\| a_{t+\tau}^{(t)} - {\hat a}_{t+\tau}^{(t-1)} \right\|_2. $$
This backward objective encourages similar latent strategies between consecutive steps while allowing for gradual adaptation to unforeseen transition dynamics.
A robust policy should predict far enough to capture temporal dependencies in demonstrations. To ensure this, we compare each candidate plan with two reference sets: one from a well-trained model as the stronger policy, and another from an early underfitting checkpoint or a shorter prediction horizon model as the weaker policy. The forward objective minimizes the average distance to positive samples from the strong policy and maximizes the average distance to negative samples from the weak policy:
$$ \mathcal{L}_F = \frac{1}{N}\left(\sum_{a^{+} \in \mathcal{A}^{+}} \sum_{\tau=0}^{l} \left\| a^{(t)}_{t+\tau} - a^{+}_{t+\tau} \right\|_2 - \sum_{a^{-} \in \mathcal{A}^{-}} \sum_{\tau=0}^{l} \left\| a^{(t)}_{t+\tau} - a^{-}_{t+\tau} \right\|_2\right),$$ where \( \mathcal{A}^{+} = \mathcal{A} \setminus \{a\} \) is the positive set predicted by the strong policy \( \pi \), \( \mathcal{A}^{-} \) is the negative set predicted by the weak policy \( \pi' \) and \(N\) is the sample size.
Consistent but unreactive to cup's motion.
Reactive but inconsistent causing jittery motion.
Reactions are slow and fails to grasp the cup firmly.
Consistent with plan and reactive to cup's motion.
We use a pretrained diffusion policy and compare the performance of BID with random sampling in open loop, random sampling in closed loop, and Exponential Moving Average (EMA) sampling. The first task is to pick up a moving cup whose initial position is fixed and place it on a nearby saucer. The cup is pulled with a string until both the gripper grasps the cup.
Our next task for the robot is to drop a toy into a plastic cup. In the dynamic setting, this cup is moved by hand as the robot carries out the task.
In simulation, we evaluate BID on the Push-T, RoboMimic, and 4-Object Franka Kitchen tasks. Below, we provide sample behaviors in stochastic environments.
Not reactive to environment stochasticity.
Reactive but not consistent with a long-term plan.
Fails to balance reactivity and long-term plan.
Reactive to stochasticity and consistent with plan.
Not reactive to stochasticity, thus unable to grab objects.
Reactive but inconsistent causing jittery motions.
Not consistent with plan causing slower movements.
Reacts to stochasticity and consistently executes plan.
Fails to react to stochasticity causing lack of precision.
Reacts to stochasticity but slow and idle trajectories.
Reacts to stochasticity but imprecise actions.
Reacts to stochasticity and consistently executes plan.
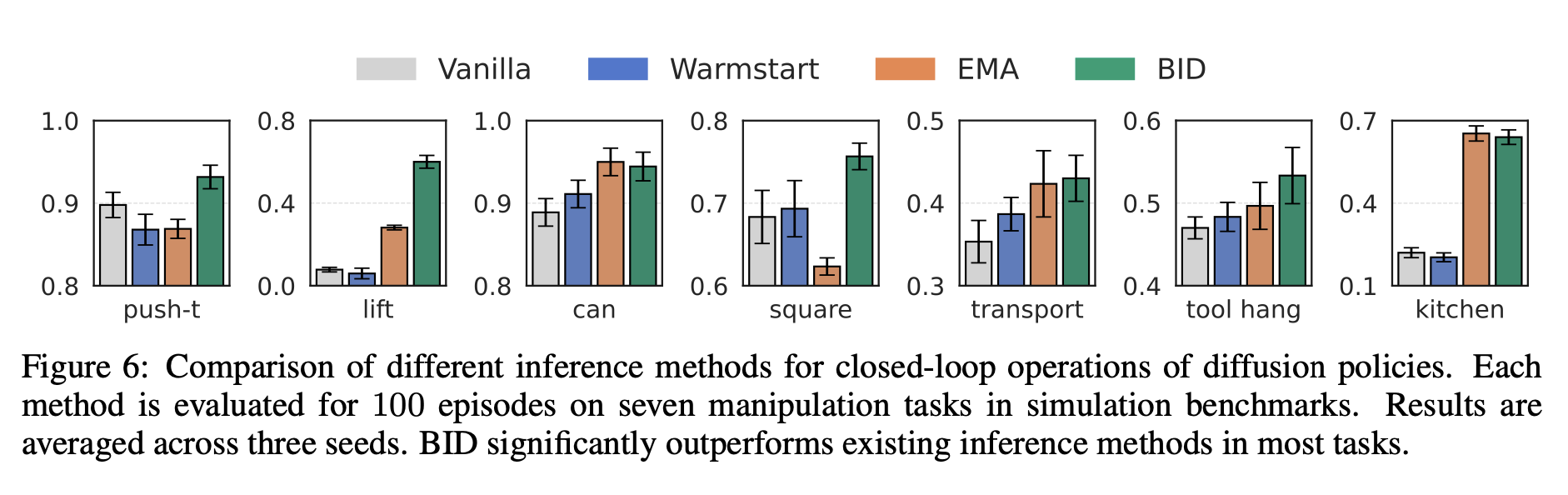
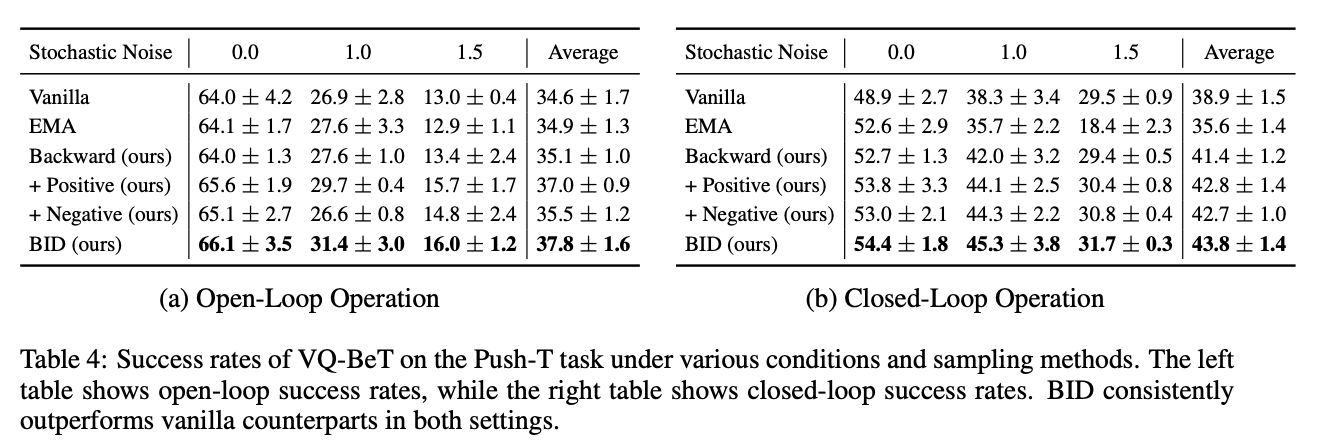
We evaluate BID on the Push-T, RoboMimic, and 4-Object Franka Kitchen tasks. While existing inference methods offer some benefits for closed-loop operations, they either lack robustness or are highly sensitive to decay rate. BID consistently achieves substantial gains across all tasks, surpassing the vanilla baseline by over 32% in relative improvements.
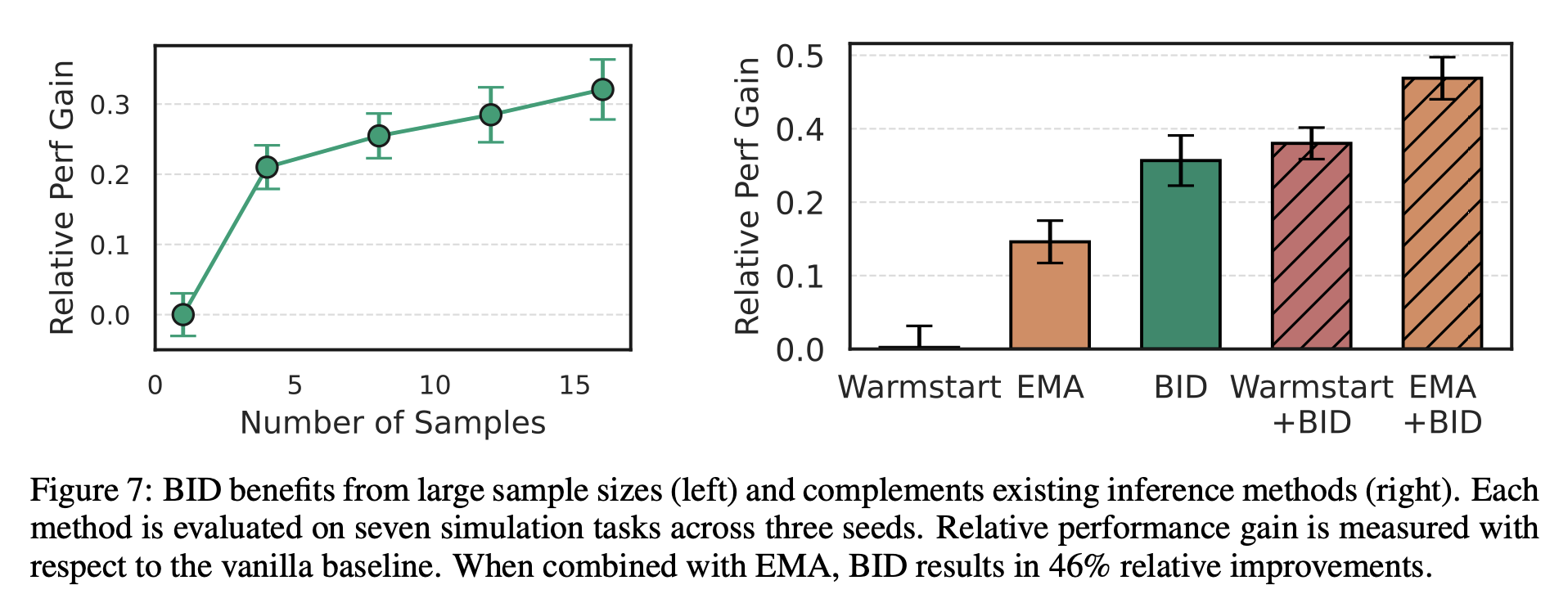
We also evaluate two critical properties of BID: scalability with increasing batch sizes and compatibility with existing inference methods. Notably, BID benefits significantly from large batch sizes, demonstrating strong potential for test-time scaling. Moreover, when combined with EMA, BID boosts the relative performance gain from 32% to 46%, exhibiting a complementary effect with existing methods.
We next extend our experiment to VQ-BET, another state-of-the-art robot policy built with autoregressive transformers, while also ablating each component of BID. We find that BID demonstrates much higher robustness to stochastic noise than other baselines and all the components of BID work synergistically to achieve the strongest performance across all environment settings.
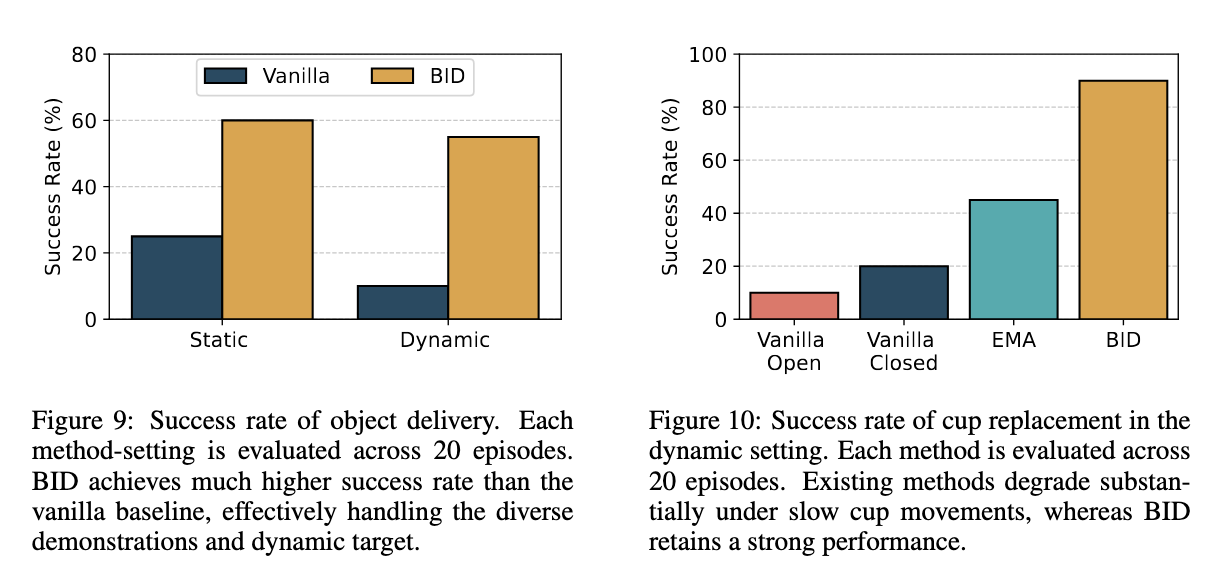
In real world, we, first, consider a task where the robot is to deliver an object held in its gripper into a cup held by a human. This task mirrors real-world scenarios where robots interact with a dynamic environment, accommodating moving objects and agents. In the second task, the robot is to pick up a moving cup and place it on a nearby saucer. BID achieves over 2x improvement in success rate compared to all other methods in the stochastic setting while matching the performance of the best alternative in the static one.
@article{liu2025bidirectional,
title={Bidirectional Decoding: Improving Action Chunking via Closed-Loop Resampling},
author={Liu, Yuejiang and Hamid, Jubayer Ibn and Xie, Annie and Lee, Yoonho and Du, Max and Finn, Chelsea},
year={2025},
journal={International Conference on Learning Representations (ICLR)},
url={https://arxiv.org/abs/2408.17355}
}